CBSE CLASS 10 BOARD 2024 ALL IMPORTANT QUESTIONS

class6,class7,class8,class9,class10,class11,class12,government jobs news,cbse update news,jobs,competition exams,india news,news update,tech news,health news,mcq questions,question answer in hindi ,question answer in english,short answer type questions,very short answer type questions,product reviews,current affairs update news ,travel blog ,education news ,govt vacancy,competition exams notification,saraswati tuition centre,exam notes,maths concept,reasoning ,exam syllabus,ncert ,practice paper

QUADRATIC EQUATION
Quadratic equations are the polynomial equations of degree 2 in one variable of type f(x) = ax2 + bx + c where a, b, c, ∈ R and a ≠ 0. It is the general form of a quadratic equation where ‘a’ is called the leading coefficient and ‘c’ is called the absolute term of f (x). The values of x satisfying the quadratic equation are the roots of the quadratic equation (α,β).
The quadratic equation will always have two roots. The nature of roots may be either real or imaginary.
The solution or roots of a quadratic equation are given by the quadratic formula:
(α, β) = [-b ± √(b2 – 4ac)]/2ac
Nature of roots:
If α and β are roots of a Quadratic Equation ax2 + bx + c then,
Question 1.
Find the roots of the equation x2 – 3x – m (m + 3) = 0, where m is a constant.
Question 2.
Find the value of p so that the quadratic equation px(x – 3) + 9 = 0 has two equal roots
Question 3..
Find the value of m so that the quadratic equation mx (x – 7) + 49 = 0 has two equal roots.
Question 4.
Find the value(s) of k so that the quadratic equation x2 – 4kx + k = 0 has equal roots.
Question5
Find the value of k for which the equation x2 + k(2x + k – 1) + 2 = 0 has real and equal roots.
Question 6.
Find the value of p for which the roots of the equation px(x – 2) + 6 = 0, are equal.
Question 7.
Solve the quadratic equation 2x2 + ax – a2 = 0 for x.
Question 8.
Find the values of p for which the quadratic equation 4x2 + px + 3 = 0 has equal roots
Question 9
Solve the following quadratic equation for x: 4x2– 4a2x + (a4 – b4) = 0
ans
∴ x =
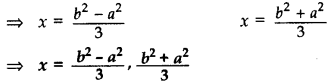
Comments
Post a Comment